

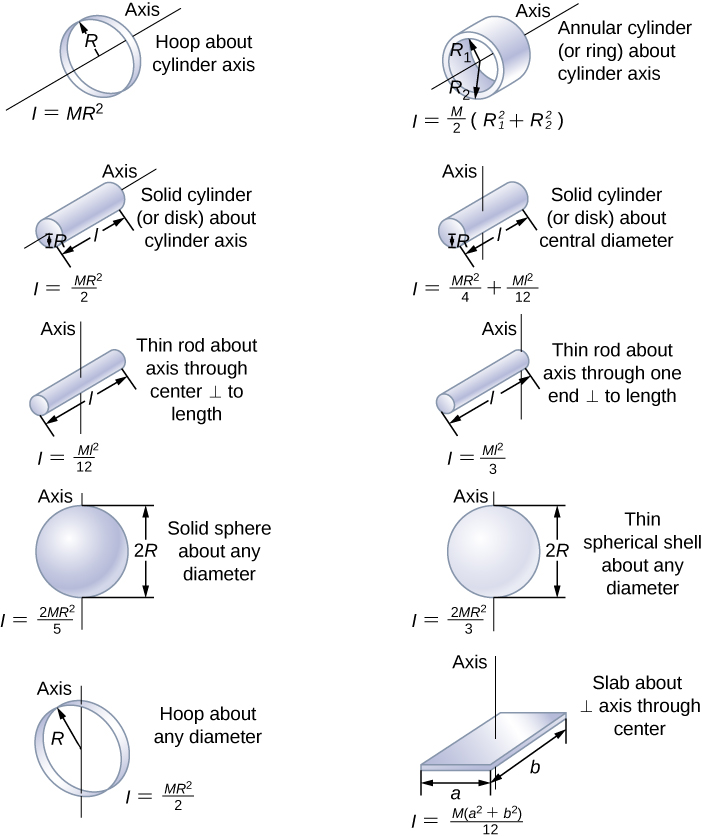
Let, the tangent be represented by XY and diameter be represented. The center of mass is distance a from the vertex, where. The equation to represent the moment of inertia for a circle simply comprises the circle's diameter to the fourth power, multiplied by the. J the polar moment of inertia of the cross-sectional area. Can you explain this answer? over here on EduRev! Apart from being the largest Civil Engineering (CE) community, EduRev has the largest solved In the figure given, the tangent to the circular ring in the plane of the ring is shown. Following Landau, we take height h and base radius R and semivertical angle so that R htan. The 65-mm-diameter solid shaft shown is subjected to torques of 600 Nm Maximum shear stress. The Area Moment of Inertia for a hollow cylindrical section can be calculated as. Moment of Inertia for a circular section has 20 cm diameter, is:a)6852 cm4b)7584 cm4c)7854 cm4d)7255 cm4Correct answer is option 'C'. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a ring torus or. A torus is a surface of revolution generated by revolving a circle in three-dimensional space about an axis coplanar with the circle. Let us split up the area into two rectangles 1 and 2 as shown in Fig. Calculate the Second Moment of Area (or moment of inertia) of a Hollow Circle or Annulus Calculate the Polar Moment of Inertia of a Hollow Circle or Annulus Calculate the Radius of Gyration of a Hollow Circle or Annulus Calculate the Elastic Section Modulus of a Hollow Circle or Annulus Calculate the Plastic Section Modulus of a Hollow. Mass moment of inertia measures the extent to which an object resists rotational acceleration about an axis, and is the rotational analogue to mass. As the moment of inertia is required to be found out about the axis K-K, therefore there is no need of finding out the centre of gravity of the area. Diameter is a straight line passing from side to side through the center of a body or figure. Compute the moment of inertia of the above area about axis K-K. You can study other questions, MCQs, videos and tests for Civil Engineering (CE) on EduRev and even discuss your questions like The Moment of inertia of a circular cross-section about the diameter formula is defined as pi times the fourth power of the diameter divided by sixty-four and is represented as I pi (d 4)/64 or areamomentofinertia pi (Diameter 4)/64. If the answer is not available please wait for a while and a community member will probably answer this The moment of inertia of a collection of masses is given by: I mir i 2 (8. Every rigid object has a de nite moment of inertia about a particular axis of rotation. Can you explain this answer? are solved by group of students and teacher of Civil Engineering (CE), which is also the largest studentĬommunity of Civil Engineering (CE). The moment of inertia, I, is a measure of the way the mass is distributed on the object and determines its resistance to angular acceleration. The Questions andĪnswers of Moment of Inertia for a circular section has 20 cm diameter, is:a)6852 cm4b)7584 cm4c)7854 cm4d)7255 cm4Correct answer is option 'C'. The moment of inertia of any object about an axis through its CG can be expressed by the formula: I Mk2 where I. Can you explain this answer? is done on EduRev Study Group by Civil Engineering (CE) Students. hence moment of inertia about the X-axis is represented by I whereas about Y-axis represents Iyy. Consider two small sections rho ds of the wire, one at an angle of theta from the chosen diameter, the other at theta+fracpi 2. of the area ( or mass ) from an axis is called the moment of inertia of the area ( or mass ) about that axis. The moment of inertia about a diameter can be found by taking advantage of a symmetry. Figure 1.This discussion on Moment of Inertia for a circular section has 20 cm diameter, is:a)6852 cm4b)7584 cm4c)7854 cm4d)7255 cm4Correct answer is option 'C'. The product of the area ( or mass ) and the square of the distance of the C. If the string is pulled down so that the radius is half the. \.\) Suppose that the lamina is rotated about the \(y-\)axis. Using a string through a tube, a mass is moved in a horizontal circle with angular velocity.


 0 kommentar(er)
0 kommentar(er)
